本文概述
基本块的DAG是有向无环图, 在节点上带有以下标签:
- 图的叶子由唯一标识符标记, 该标识符可以是变量名或常量。
- 图的内部节点由运算符标记。
- 还为节点提供了一系列标识符, 以供标签存储计算值。
- DAG是一种数据结构。它用于在基本块上实现转换。
- DAG提供了一种确定公共子表达式的好方法。
- 它给出了该语句所计算的值如何在后续语句中使用的图形表示。
DAG的构建算法
输入:它包含一个基本块
输出:它包含以下信息:
- 每个节点都包含一个标签。对于叶子, 标签是标识符。
- 每个节点都包含一个附加标识符列表, 以保存计算值。
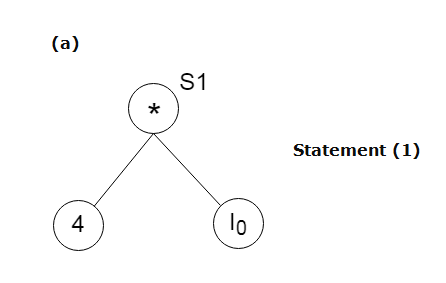
Case (i) x:= y OP z
Case (ii) x:= OP y
Case (iii) x:= y方法
步骤1:
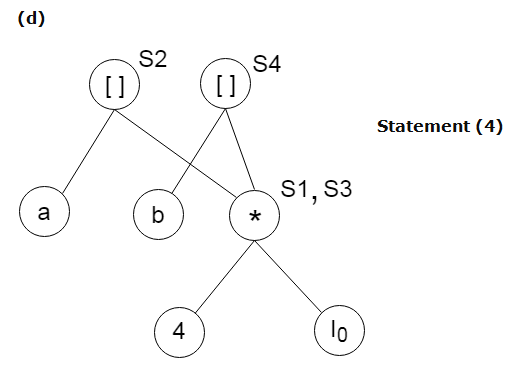
如果未定义y操作数, 则创建node(y)。
如果未定义z操作数, 则为case(i)创建node(z)。
第2步:
对于情况(i), 创建节点(OP), 其右子节点为node(z), 左子节点为node(y)。
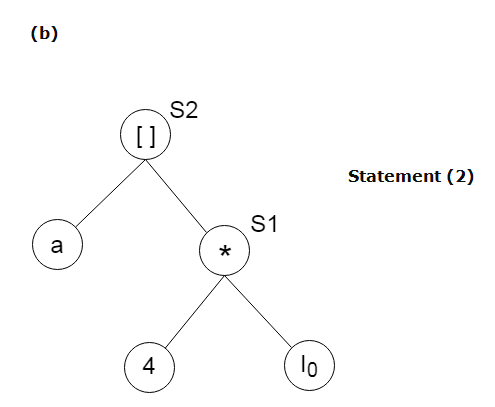
对于情况(ii), 检查是否有一个子节点(y)的节点(OP)。
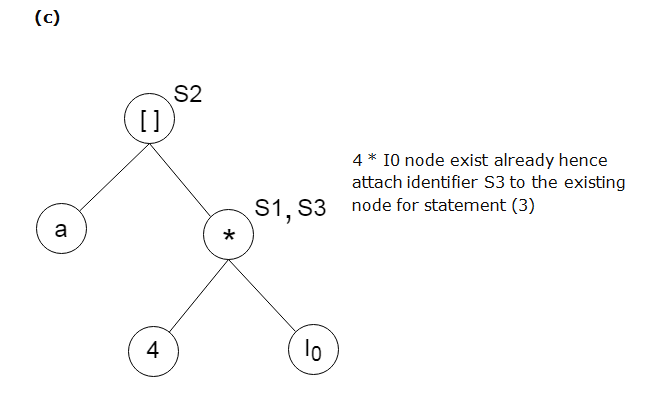
对于情况(iii), 节点n将是节点(y)。
输出:
对于node(x), 从标识符列表中删除x。将x附加到步骤2中找到的节点n的附加标识符列表中。最后将node(x)设置为n。
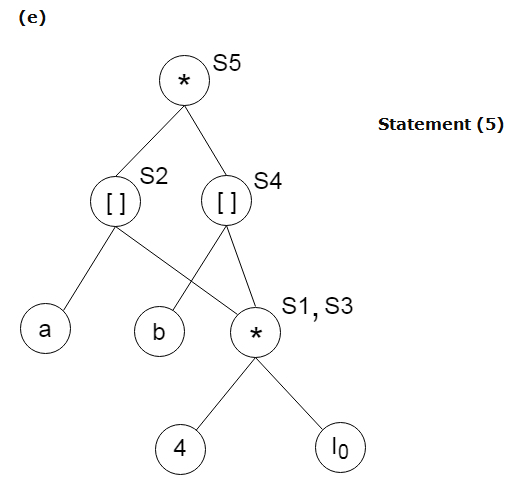
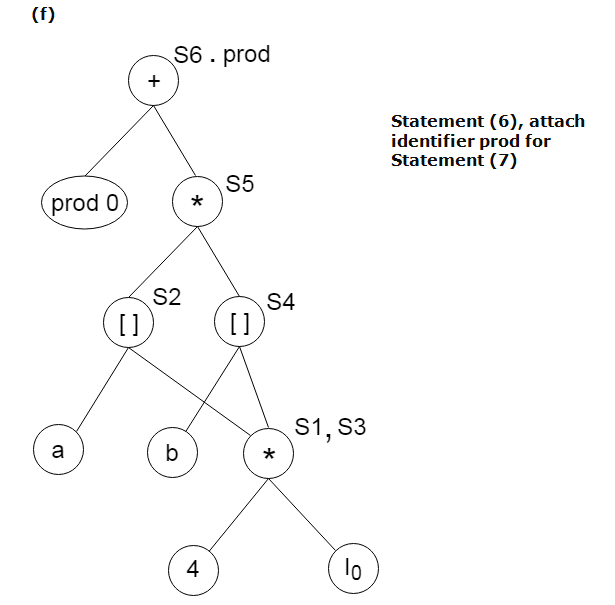
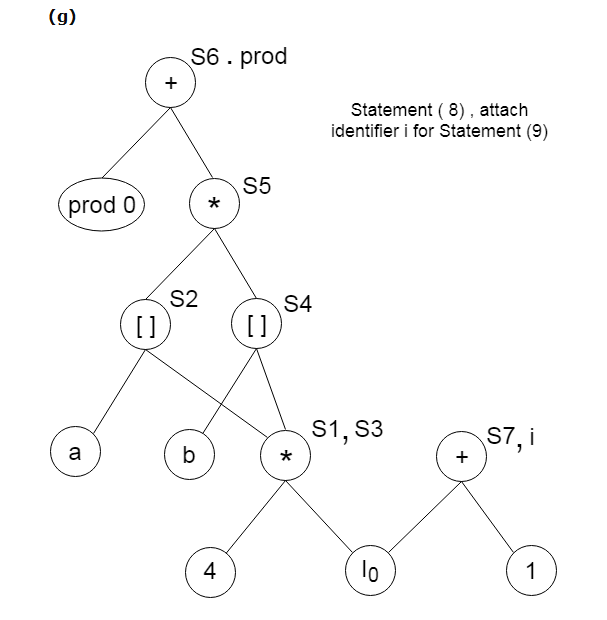
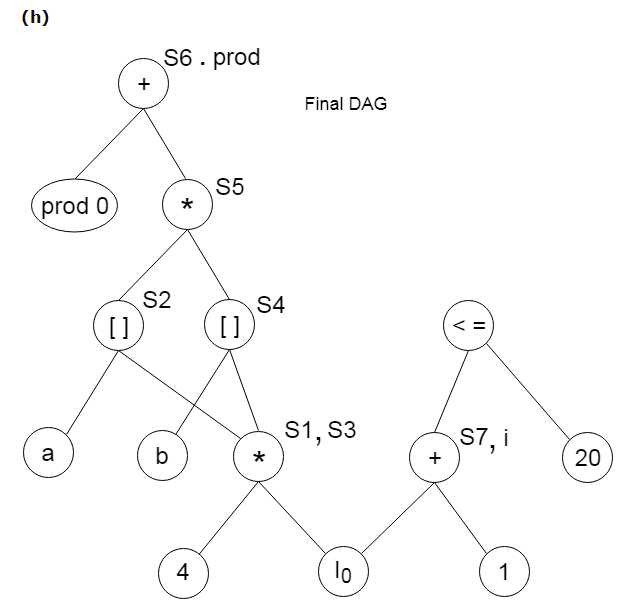
例:
考虑以下三个地址声明:
S1:= 4 * i
S2:= a[S1]
S3:= 4 * i
S4:= b[S3]
S5:= s2 * S4
S6:= prod + S5
Prod:= s6
S7:= i+1
i := S7
if i<= 20 goto (1)DAG建设实习:
 srcmini
srcmini
评论前必须登录!
注册